Didier Badouel's Ray-Triangle Intersection Algorithm

27 Apr 2015 $\newcommand{\point}[1]{\boldsymbol{#1}} \newcommand{\vector}[1]{\overrightarrow{\boldsymbol{#1}}}$

Lightbox will only support triangle meshes for now, which means that a whole lot of ray-triangle intersections have to be done. Thus, we want to make sure that ray-triangle intersection is fast. This post will focus on analyzing a method first published in 1990 by Didier Badouel in a chapter in the Graphics Gems I book, called “An efficient ray-polygon intersection”. The algorithm allows for calculating the intersection point of a ray with an arbitrary polygon. We will make that more specific by only focusing on triangle intersection.

Step 1: Finding the intersection of a ray with a plane

We will first focus on finding the intersection of a ray with the plane through a triangle $T$ . A point $R$ on the ray is defined as:

$\point{R}(t) = \point{O} + \vector{D}t$

where $\point{O}$ is the origin of the ray, and $\vector{D}$ is the direction of the ray. Finding the intersection point of the ray with triangle $T$ boils down to finding the value for $t$ for which $\point{R}(t)$ lies on the triangle surface.

The triangle $T$ is made up of three vertices $V_i$ , with $0 \leq i < 3$ . Thus, $T$ consists of three edges $\vector{V_0V_1}$ , $\vector{V_0V_2}$ , and $\vector{V_1V_2}$ . The normal $\vector{N}$ of $T$ is defined as:

$\vector{N} = \vector{V_0V_1} \times \vector{V_0V_2}$

The plane through $T$ is defined as the set of points $\point{P}$ for which $\vector{N} \cdot (\point{P} - \point{V_0}) = 0$ holds. In other words, all points $\point{P}$ for which the vector from $\point{V_0}$ to $\point{P}$ is perpendicular with $\vector{N}$ .

We can rephrase this as:

$\begin{eqnarray} 0 &=& \vector{N} \cdot (\point{P} - \point{V_0}) \\ &=& \vector{N} \cdot \point{P} - \vector{N} \cdot \point{V_0} \\ &=& \vector{N} \cdot \point{P} - D \\ &=& A P_x + B P_y + C P_z - D \end{eqnarray}$

which results in the plane equation for the plane through $T$ . Here, $A$ , $B$ , and $C$ are the $x$ , $y$ , and $z$ components of the normal $\vector{N}$ , and $D = \vector{N} \cdot \point{V_0}$ . Finding the value for $t$ for which $R(t)$ lies on the plane that goes through thetriangle $T$ now boils down to finding the solution for the equation:

$\begin{eqnarray} \vector{N} \cdot \point{R}(t) - D &=& 0 \\ \end{eqnarray}$

Substituting $\point{O} + \vector{D}t$ for $R(t)$ yields:

$\vector{N} \cdot (\point{O} + \vector{D}t) - D = 0$

Solving for $t$ results in:

$t = \frac{-\vector{N} \cdot \point{O} + D}{\vector{N} \cdot \vector{D}}$

In case $\vector{N} \cdot \vector{D} = 0$ , the ray is parallel with the plane, and there is no single intersection point. We have found an intersection with the plane that goes through the triangle in case $t > 0$ . In practice, we need to check for $t > \epsilon$ for some small value $\epsilon$ , otherwise, a ray originating from a triangle surface might self-intersect with the triangle it is originating from.

Step 2: Intersecting the triangle

In the second step, Badouel explains how to determine whether the intersection point with the plane through the triangle found in step 1 actually lies within the triangle boundaries. Any point $\point{P}$ within the triangle $T$ can be represented as follows:

$\begin{eqnarray} \vector{V_0P} &=& \alpha \vector{V_0V_1} + \beta \vector{V_0V_2} \tag{0} \label{0} \\ \end{eqnarray}$

This is further illustrated in the figure below which can also be found in Badouel’s description of the algorithm:

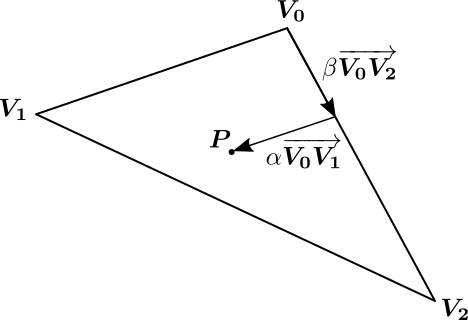^{_{Parametric representation of the point $\point{P}$}}

The point $\point{P}$ is inside the triangle in case $\alpha \geq 0$ , $\beta \geq 0$ , and $\alpha + \beta \leq 1$ . Here, $(\alpha, \beta)$ is the so-called Barycentric coordinate of $\point{P}$ .

To see whether $\point{P}$ lies within the boundaries of the triangle, we thus have to check whether $\alpha \geq 0$ , $\beta \geq 0$ , and $\alpha + \beta \leq 1$ holds. Equation $\eqref{0}$ gives rise to the following system of equations:

$\left\{ \begin{eqnarray} P_x - V_{0_x} & = & \alpha(V_{1_x} - V_{0_x}) + \beta(V_{2_x} - V_{0_x}) \\ P_y - V_{0_y} & = & \alpha(V_{1_y} - V_{0_y}) + \beta(V_{2_y} - V_{0_y}) \\ P_z - V_{0_z} & = & \alpha(V_{1_z} - V_{0_z}) + \beta(V_{2_z} - V_{0_z}) \\ \tag{1} \label{1} \end{eqnarray} \right.$

Badouel now simplifies this system of equations by projecting the triangle on one of the primary planes $xy$ , $xz$ , or $yz$ . Here, Badouel uses the fact that after projecting a triangle, the Barycentric coordinate $(\alpha, \beta)$ of $\point{P}$ does not change. A requirement for this is that the projected triangle does not degenerate to a line. Thus, we need to make sure that we do not project the triangle on a plane perpendicular to the triangle. To avoid this situation, the dominant axis of the triangle’s normal is determined, and the triangle is projected on the plane perpendicular to that axis. Note that by taking the dominant axis, the area of the projected triangle is as large as possible, avoiding numerical errors. Now, assuming that the X-axis is the dominant axis of the triangle, projecting on the $yz$ plane then reduces $\eqref{1}$ to:

$\left\{ \begin{eqnarray} P_y - V_{0_y} & = & \alpha(V_{1_y} - V_{0_y}) + \beta(V_{2_y} - V_{0_y}) \\ P_z - V_{0_z} & = & \alpha(V_{1_z} - V_{0_z}) + \beta(V_{2_z} - V_{0_z}) \\ \tag{2} \label{2} \end{eqnarray} \right.$

To generalize this, assume that $\vector{N}$ is the normal of the triangle. We determine $i_0$ such that:

$i_0 = \left\{ \begin{eqnarray} 0 \quad \text{if} \quad |N_x| & = & \max(|N_x|, |N_y|, |N_z|) \\ 1 \quad \text{if} \quad |N_y| & = & \max(|N_y|, |N_y|, |N_z|) \\ 2 \quad \text{if} \quad |N_z| & = & \max(|N_z|, |N_y|, |N_z|) \\ \end{eqnarray} \right.$

Furthermore, assume that $i_1$ and $i_2$ are the indices different from $i_0$ , with $i_1, i_2 \in \{0, 1, 2\}$ . Projecting $\vector{V_0P}$ , $\vector{V_0V_1}$ , and $\vector{V_0V_2}$ results in three two-dimensional vectors $\vector{a}$ , $\vector{b}$ , and $\vector{c}$ respectively on the projection plane:

$\begin{eqnarray} \vector{a} & = & \begin{pmatrix}P_{i_1} - V_{0_{i_1}}\\P_{i_2} - V_{0_{i_2}}\end{pmatrix} \qquad \vector{b} & = & \begin{pmatrix}V_{1_{i_1}} - V_{0_{i_1}}\\V_{1_{i_2}} - V_{0_{i_2}}\end{pmatrix} \qquad \vector{c} & = & \begin{pmatrix}V_{2_{i_1}} - V_{0_{i_1}}\\V_{2_{i_2}} - V_{0_{i_2}}\end{pmatrix} \end{eqnarray}$

We can use this to rewrite $\eqref{2}$ for the general case:

$\vector{a} = \alpha\vector{b} + \beta\vector{c}$

Which can be rewritten in matrix multiplication form as follows:

$\begin{pmatrix}b_u & c_u \\ b_v & c_v\end{pmatrix} \begin{pmatrix}\alpha \\ \beta\end{pmatrix} = \begin{pmatrix}a_u \\ a_v\end{pmatrix}$

We use the subscripts $u$ and $v$ here for the two dimensions of the projection plane. Solving this using Cramer’s rule results in:

$\alpha = \frac{\begin{vmatrix}a_u & c_u \\ a_v & c_v\end{vmatrix}}{\begin{vmatrix}b_u & c_u \\ b_v & c_v\end{vmatrix}} \qquad \beta = \frac{\begin{vmatrix}b_u & a_u \\ b_v & a_v\end{vmatrix}}{\begin{vmatrix}b_u & c_u \\ b_v & c_v\end{vmatrix}}$

We can now trivially check whether the intersection point $\point{P}$ is within the triangle boundaries. In the next article I will look at the ray-triangle intersection proposed by Ingo Wald, which improves upon this algorithm.